The Reef
A downloadable game for Windows, macOS, Linux, and Android
Welcome to The Reef!
Check out our simulation game of an ecosystem surrounding coral reef. Ecosystems are finely tuned to maintain balanced populations of predators, and prey. Tip one little component out of place and the whole system can collapse! To capture the fragility of real world ecosystems, our game simulates the interactions between two competing animal populations by leveraging real world biology and mathematics to create a simulation of how predators and prey populations interact with each other. It’s up to you to keep both the predators and the prey of The Reef Alive!
Cause Collapse or Explosion!
The fate of the animals living in The Reef lies in your hands. Manage and balance the populations of various predator and prey species, by controlling the parameters of the simulation. You have access to four buttons on the lower left of the screen, that control birth rate, death rate, the consumption of prey, and the probability of predators and prey interacting. Control these parameters and watch the ecosystem collapse or the population explode!

Battle Man-Made Disasters
Use your control over the ecosystem to combat the negative effects of man-made disasters. These events range from coral bleaching, to overfishing. Try to combat these events or watch the effects play out in real time.
Let us know what you think
Please try out or game and comment to tell us what you think! Our approach to the theme of “Keep it Alive”, was centered on how do you keep two populations alive when those populations can negatively affect each other. Rather than thinking about how to keep a single individual or group alive we thought about how species survive and thrive over time what kind factors influence that. We hope that our game demonstrates how difficult and exciting it can be trying to keep two groups of animals alive simultaneously.
A look at the Math
The equations that drive the simulation are known as The Lotka–Volterra system of equations. This system is comprised of two differential equation that describe the change in a population over time. These equations are linked in such a way that a change in one affects the other! Below are the equations our simulation generates data of off:
Prey:
- dx/dt = b x - h x * y Predators:
- dy/dt = c h x y - d y
The parameters above are:
- b: The prey birth rate
- d: The predator death rate
- h: The interaction rate between the two populations
- c: The conversion rate from prey to predators
- x: The number of prey
- y: The number of predators
By integrating over these equations with respect to time we can find the population at a given time, like the graph below!
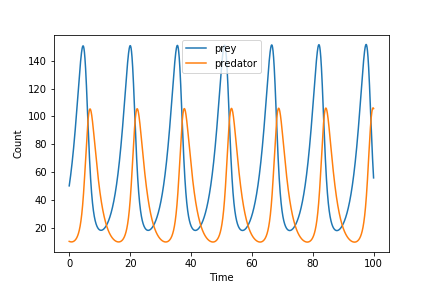
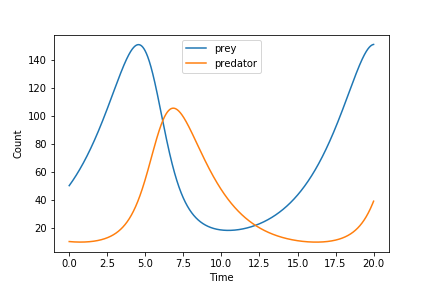
AS you can see the populations of prey and predators “chase” each other over time. As the number of prey increase, there is more food for the predators and thus their population will grow until they deplete the prey population and can no longer support their own population. below is a zoomed in version of the plot above that shows the inflection point where the predator population grows to large and cause the prey population to fall rapidly. (You can see these graphs play out in real time with actual populations in the game!)
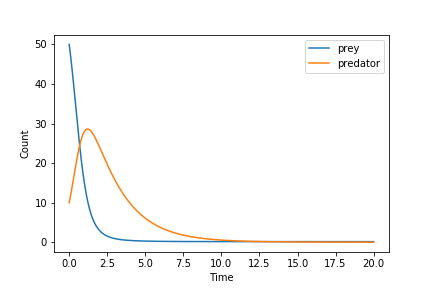
What happens when we mess with the parameters, below are some examples of what can happen when things get thrown out of balance. Below is an example where the birth rate of prey was set to zero thus causing the predators to die off suddenly!
And this is an example of what happens when we set the predator death rate to zero, or in english making the predators of the system immortal!
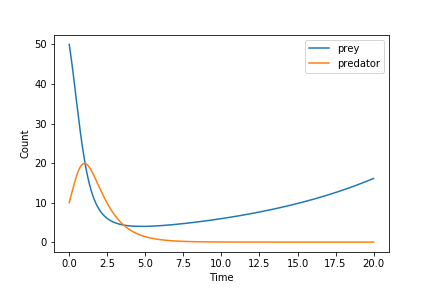
Unstable systems like these can happen due to the simulated disasters we built into the game. Try control the different parameters to combat the collapse !
| Status | Released |
| Platforms | Windows, macOS, Linux, Android |
| Author | jakemchugh1 |
| Genre | Simulation |
| Tags | Ludum Dare 46 |
| Links | Ludum Dare |
Leave a comment
Log in with itch.io to leave a comment.